تحقیق در قضیه پیک

تحقیق در قضیه ی پیک

ممکن است دانش آموزان در دوره ی راهنمایی، قضیه ی پیک را دیده باشند. دانش آموزان در این مجموعه از دروس، دوباره با قضیه ی پیک آشنا شده و از جبر برای تعیین ضرایب معادله استفاده می کنند و مفهوم آهنگ را به عنوان ساز و کاری برای یافتن ضرایب قضیه ی پیک، می آموزند.

 

محتوای ریاضی

1. دستگاه معادلات
2. آهنگ تغییرات

هر چند در این مجموعه از دروس، ارتباط و شیوه های مختلف ارائه، در درس جداگانه ای مطرح نشده اما در همه ی دروس، زمینه ای فراهم شده تا دانش آموزان با دادن ایده های ریاضی و به کار بردن شیوه های مختلف ارائه برای سازمان دهی به کارهایشان، بر استانداردهای ارائه و ایجاد ارتباط متمرکز شوند.

 

دروس

درس اول:  کشف الگوها در قضیه ی پیک

 این درس، با استفاده از یک تخته ی میخی و یا اپلت تخته میخی، دانش آموزان می توانند الگوهای قضیه ی پیک را بیابند.

اهداف

پس از تکمیل این درس دانش آموزان می توانند:

اشکال مختلف روی تخته ی میخی را برای تعیین رابطه ی بین تعداد نقاط محیطی، تعداد نقاط داخلی و مساحت شکل بررسی کنند.

با استفاده از علامت های جبری برای نمایش این رابطه، معادله بسازند.

وسایل لازم

تخته ی میخی و نوار یا مدل سازی تخته میخی

برگه ی فعالیت کشف قضیه ی پیک

طرح درس

در درس اول، قضیه ی پیک برای دانش آموزانی که با این قضیه آشنا نیستند، تدریس و برای دانش آموزانی که با آن آشنا هستند، یادآوری می شود.

یکی از انواع تخته های میخی را در اختیار دانش آموزان قرار دهید. تخته ی میخی و نوارهای لاستیکی و یا تخته ی میخی مقوایی. اگر به رایانه دسترسی دارید، می توانید از مدل سازی تخته ی میخی نیز استفاده کنید. از دانش آموزان بخواهید با کمک نوارهای لاستیکی چند شکل بسازند. سپس توجه آن ها را به تعداد نقاط محیطی (P) و نیز تعداد نقاط داخلی (A) هر شکل جلب کنید. می توان دانش آموزان را تشویق کرد تا برای ثبت یافته های خود با این داده ها نمودار تهیه کنند.

ممکن است محاسبه ی درست مساحت شکل، در ابتدای فعالیت برای دانش آموزان دشوار باشد. پیش از این مرحله، توضیح دهید شکل را به مستطیل های کوچک تقسیم کنند. این کار به آن ها کمک می کند تا بتوانند مساحت شکل را آسان تر حساب کنند.

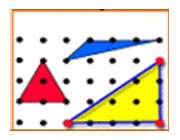
برای مثال برای تعیین مساحت مثلث زیر، می توان ابتدا مساحت مربع محیط بر آن را محاسبه و سپس مساحت قسمت های اضافی را از آن کم کرد.

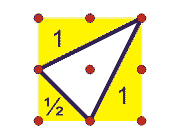
مساحت این مربع، 4 واحد مربع است و مساحت کل قسمت های اضافی 2.5 واحد مربع است. در نتیجه مساحت مثلث 1.5=2.5-4 واحد مربع است.

 

برگه ی فعالیت کشف قضیه ی پیک را بین دانش آموزان پخش کنید و به دانش آموزان کمک کنید تا بررسی خود را شروع کنند. پرسش های 1 تا 5، پرسش های اساسی و پایه ای این فعالیت است و در پرسش های 6 تا 14، به دانش آموزان کمک می شود تا گام به گام این فعالیت را انجام دهند. (می توان برگه های فعالیت را یکی یکی به شاگردان داد و برگه های بعدی را پس از انجام مراحل قبلی بین آن ها توزیع کرد.)

 

برگه ی فعالیت کشف قضیه ی پیک

این برگه، طوری طراحی شده است تا دانش آموزان به طور مداوم با فرضیات شخصی و فرموله کردن این فرضیات در گروه خود، مشغول باشند. با گروه بندی دانش آموزان، اعضای گروه نتایج محاسبات هم گروهی های خود را کنترل می کنند.

در پایان این فعالیت، دانش آموزان باید به فرمول زیر در قضیه ی پیک، برسند.

A = 1/2 P + I – 1

 

همچنین می توانید فعالیت پژوهشی در مفهوم مثلث و خواص چند ضلعی ها: ساخت چند ضلعی ها را با دانش آموزان انجام دهید.

پرسش هایی برای دانش آموز

چگونه می توان مساحت شکل های نامنظم را محاسبه کرد؟

[یکی از روش های محاسبه ی مساحت اشکال نامنظم، استفاده از قضیه ی پیک است؛ البته با این فرض که می توان این اشکال را طوری بر روی صفحه ی مختصات قرار داد که رئوس شکل بر نقطه های مختصاتی منطبق شوند.]

مساحت اشکال مختلف در صورت داشتن تعداد نقاط محیطی متفاوت و تعداد نقاط داخلی یکسان چه رابطه ی با هم دارند؟ تغییر تعداد نقاط محیطی چه ت?ثیری دارد؟

[وقتی تعداد نقاط محیطی 1 واحد افزایش می یابد، مساحت به اندازه 2/1 تعداد نقاط محیطی زیاد می شود.]

مساحت اشکال مختلف در صورت داشتن تعداد نقاط داخلی متفاوت و تعداد نقاط محیطی یکسان چه رابطه ی با هم دارند؟ تغییر تعداد نقاط داخلی چه ت?ثیری دارد؟

[وقتی تعداد نقاط داخلی 1 واحد افزایش می یابد، مساحت به اندازه ی 1 واحد زیاد می شود.]

 

ارزشیابی

می توان از دانش آموزان خواست تا ارزیابی خود را درباره ی فرایند کشف، توانایی تولید اشکال با تعداد میخ های محیطی و داخلی بنویسند و مشخص کنند بحث های گروهی چه مقدار به پدیدار شدن سریع تر معادله کمک می کند.

 

توسعه

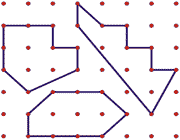
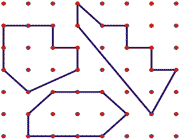
1- اگر فرصت هایی برای دانش آموزان ایجاد کنید که با P و A معلوم، اشکال ابتکاری بسازند، از این کار لذت می برند. برای مثال، از آن ها بخواهید تا اشکالی بسازند که 9 نقطه ی محیطی و 3 نقطه ی داخلی دارد. (برخی از اشکال ممکن، در زیر آورده شده است.)

2- برای ایجاد معادله، از دانش آموزان بخواهید تا مساحت اشکال را با استفاده از چند مکعب بیابند. (چون ممکن است در مساحت بعضی از اجسام 2/1 وارد شود، از آن ها بخواهید تا دو مکعب را به عنوان واحد مساحت استفاده کنند.) از آن ها بخواهید تا این مکعب را طوری روی محورهای مختصات قرار دهند که P روی محور x و I بر روی محور y باشد. بنابراین شکلی با مساحت 6.5 باید در نقطه ی (3، 9) باشد. با این نمودار دانش آموزان می توانند ببینند با ثابت نگه داشتن P یا I مساحت شکل چه تغییری می کند.

3- از دانش آموزان بخواهید تا به کمک یک برگه ی نقطه چین، مساحت اشکال نامنظم را تخمین بزنند. از آن ها بخواهید اشکالی را که خود رسم می کنند، بررسی کنند. چند شکل در حالت های خاص نیز خودتان برای آن ها ترسیم کنید.

 

بررسی اجرای طرح درس در کلاس

آیا از برگه ی فعالیتی استفاده کردید؟ آیا برگه ی فعالیتی ساختارهای زیادی را مهیا می کند؟ ترجیح می دهید در جلسات آموزشی بعدی، تنها از نصف ساختارهای موجود در برگه ی فعالیتی استفاده کنید؟

آیا در محاسبه ی مساحت اشکال با تعداد اضلاع فرد، دانش آموزان به راهنمایی های بیشتری نیاز دارند؟ آیا در جلسه های آموزشی بعدی برای اجرای این روش، ابتدا تعیین مساحت مثلث را یادآوری می کنید؟

آیا برای تحقق اهداف این درس، طرح درس را تغییر دادید و اصلاحاتی در آن انجام دادید؟ اگر این کار را کردید برای این که دانش آموزان درس را بفهمند، چه فعالیت دیگری پیشنهاد می کنید؟

 

درس دوم:  قضیه ی پیک به عنوان دستگاه معادلات

اهداف

دانش آموزان پس از تکمیل این درس می توانند:

سه شکل بسازند و تعداد نقاط محیطی، نقاط درونی و مساحت آن را پیدا کنند.

از داده ها برای ایجاد دستگاه معادله استفاده کنند.

با کمک روابط جبری، دستگاه معادلات را حل کرده و ضریب قضیه ی پیک را بیابند.

 

وسایل لازم

تخته ی میخی و نوارهای لاستیکی (یا چیزی شبیه به آن)

طرح درس

مسئله ی اصلی در این درس، تعیین مقادیر ضرایب و عبارت ثابت در قضیه ی پیک است. به ویژه، تعیین مقادیر ضرایب a و b و نیز ثابت c در معادله ی زیر:

c + (تعداد میخ های داخلی) b + (تعداد میخ های محیطی) a = مساحت

یا به شکل ساده تر:

A = aP + bI + c

شاید بهتر باشد ابتدا درباره ی تفاوت میان ضرایب a، b و c و متغیرهای P و I بحث کنیم. دانش آموزان باید بدانند که a، b و c فقط علایمی برای نمایش کلی مقادیری هستند که در مسئله ای خاص، معلومند، در حالی که P و I مجهول های واقعی اند.

این مسئله مانند تعیین سهمی با سه نقطه ی معلوم است. اما به نظر می رسد این فعالیت برای بیشتر دانش آموزان جالب تر است.

از دانش آموزان بخواهید تا بر روی تخته ی میخی سه شکل مختلف بسازند که تعداد نقاط محیطی، تعداد نقاط درونی و مساحت آن ها با هم متفاوت باشد. (دانش آموزان می توانند از تخته ی میخی، کاغذهای نقطه چین و یا اپلت تخته ی میخی استفاده کنند.)  همان گونه که در بخش کشف الگوی قضیه ی پیک اشاره شد، مشکل ترین بخش، تعیین صحیح مساحت است. ممکن است در این مرحله، دانش آموزان برای اطمینان از درستی محاسبات خود، پاسخ های هم کلاسی های خود را امتحان کنند.

دانش آموزان با سه شکل و مقادیر P، I و A مربوط به این اشکال، می توانند یک دستگاه سه معادله ای ایجاد و آن را حل کنند.

برای مثال، سه شکل با مقادیر زیر را در نظر بگیرید:

با این مقادیر، دستگاه سه معادله ای زیر حاصل می شود:

P = 4, I = 0, A = 1

P = 8, I = 1, A = 4

P = 8, I = 4, A = 7

 که می توان آن را به شکل زیر نوشت:

1 = a(4) + b(0) + c

4 = a(8) + b(1) + c

7 = a(8) + b(4) + c

 

به عبارت دیگر، a = 1/2، b = 1 و c = -1 .بنابراین قضیه ی پیک به صورت زیر است:

1 =(a(2) + b(0) + c(0

1 = (a(0) + b(1) + c(0

1 = (a(0) + b(0) + c(-1

علاوه بر روشی که در بالا استفاده شد، روش ترکیب خطی یا ماتریس ها را نیز می توان به کار برد. (در روش ماتریس ها، استفاده از ماشین حساب گرافیکی مفید است). دستگاه معادلات به شکل ماتریسی، به صورت زیر نشان داده می شود:

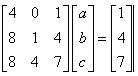
برای یافتن ضرایب، به صورت زیر، معکوس ماتریس ضرایب را در ماتریس اعداد ثابت ضرب کنید. با این کار نتایج زیر حاصل می شود:

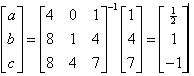
همان طور که این رابطه نشان می دهد، a = 1/2، b = 1 و c = -1 است.

سپس از دانش آموزان بخواهید تا شکل های یکدیگر را امتحان کنند تا مطمئن شوند معادله هایشان درست جواب می دهد. ممکن است در هنگام انجام عملیات ریاضی، دستگاه معادلات یا تعیین مساحت اولیه اشتباهاتی رخ دهد که هر کدام از اشتباهات باعث ایجاد فرمول نادرستی می شود.

 

پرسش هایی برای دانش آموزان

همان طور که مشاهده کردید، تنها تعداد نقاط محیطی و نقاط درونی برای تعیین مساحت اشکال مورد استفاده قرار گرفت، پس چرا سه متغیر در معادله وجود دارد؟

[متغیر سوم، ثابت معادله را نشان می دهد. این متغیر، ضریب نیست.]

چرا از شما خواسته شد تا سه شکل بسازید. آیا می توان این فعالیت را با دو شکل انجام داد؟ با چهار شکل چطور؟

[در معادله، سه مجهول a، b و c وجود دارد. برای تعیین مقادیر سه مجهول، حداقل به سه معادله نیاز است؛ بنابراین دو شکل کافی نیست. با چهار شکل، می توان به نتیجه رسید ولی یک شکل، اضافی است.]

حالتی را توضیح دهید که یکی از دانش آموزان ممکن است تصور کند سه شکل مجزا ساخته؛ اما در واقع فقط دو شکل ساخته است. یعنی در چه حالتی، دانش آموز فکر می کند مثال کافی دارد، اما نمی تواند دستگاه معادله را حل کند؟

[ممکن است در اشکالی که دانش آموز استفاده می کنند، تعداد نقاط درونی و محیطی یکسان باشد. اگر این اشکال تنها به ظاهر متفاوت باشند و مقادیر P و I برای هر دو یکسان باشد، دستگاه بی نهایت جواب دارد. برای مثال، دو شکل زیر را که در هر دو P = 4 و I = 1 است در نظر بگیرید:

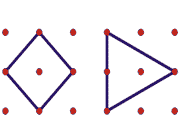
معادله ی حاصل از هر دو شکل 2 = 4a + b + c است؛ بنابراین این معادله، دو بار در سیستم ظاهر می شود. اگر این دو معادله را از هم کنید، معادله بی معنی 0 = 0 نتیجه می شود.]

ارزشیابی

از دانش آموزان بخواهید تا در نامه ای، فنون کاربردی در این درس، دلیل کاربرد آن ها و اشتباهاتی را که باید در تولید این دستگاه معادلات از آن ها اجتناب کرد، برای یکی از دانش آموزان غایب توضیح دهند.

توسعه

از دانش آموزان بخواهید تا دو نقطه روی صفحه انتخاب کنند و شیب خط و عرض از مبدأ خط حاصل از این دو نقطه را تعیین کنند. معادله ی این خط به صورت زیر است: y = ax + b. بنابراین با داشتن مقادیر x و y و جایگزین کردن آن در معادله، می توان a و b را یافت. با این کار می توان بحث خوبی را درباره ی این که چرا برای تعیین یک خط، داشتن دو نقطه الزامی است، بین دانش آموزان ایجاد کرد.

با همین روش می توان از سه نقطه برای تعیین ضرایب سهمی استفاده کرد. معادله ی سهمی به صورت زیر است: y = ax2 + bx + c . دانش آموزان می توانند با جایگزین کردن x و y در معادله، a، b و c را بیابند.

 

بررسی اجرای طرح درس در کلاس

آیا دانش آموزان متوجه شده اند که برای یافتن سه مجهول به سه معادله نیاز است؟ اگر نه، چه راهی پیشنهاد می کنید تا دانش آموزان این مسئله را بفهمند؟

آیا دانش آموزان مفهوم ضریب c، ثابت معادله و نقش آن در معادله را فهمیده اند؟ در بسیاری از موارد، آن ها تصور می کنند نیازی به محاسبه ی c نیست، زیرا تنها P و I به ضریب نیاز دارند؟ چگونه می توان مفهوم ثابت معادله را به دانش آموزان توضیح داد؟

آیا دانش آموزان در تمام مدت درگیر فعالیت بودند یا انتقال از تخته ی میخی به دفتر و مداد، موجب شد تا سرعت آن ها پایین بیاید؟ اگر بخواهید دوباره این فعالیت را انجام دهید، چگونه این مسئله را حل می کنید؟

درس سوم:  آهنگ تغییر در قضیه ی پیک

دانش آموزان از صفحه ی گسترده برای بررسی آهنگ تغییر در میان اشکال مختلف ایجاد شده بر روی تخته ی میخی استفاده می کنند. به کمک آهنگ تغییر، به راحتی می توان ضریب قضیه ی پیک را پیدا کرد.

اهداف

پس از اتمام این درس دانش آموزان می توانند:

صفحه ی گسترده ای برای بررسی قضیه ی پیک ایجاد کنند.

با تغییر مقادیر سطر و ستون به دنبال تفاوت مساحت ها بوده و با کمک آن درباره ی آهنگ تغییر بحث کنند.

 

وسایل لازم

تخته ی میخی و نوار لاستیکی (یا وسیله ی دیگری)

صفحه ی گسترده ی قضیه ی پیک

رایانه با برنامه ی صفحه گسترده (اختیاری)

 

هدف این درس، کاربرد صفحه ی گسترده به عنوان ابزار مشاهده ی الگوها در چندین خانه ی جدول است. از آن جا که مساحت به دو متغیر یعنی تعداد نقاط داخلی و محیطی وابسته است، استفاده از شیوه ی ارائه صفحه ی گسترده، طبیعی است.

وقتی از تخته ی میخی فیزیکی استفاده می کنید، دانش آموزان به طور طبیعی بر روی نقاط محیطی متمرکز می شوند، زیرا افزایش مقادیر نقاط محیطی آسان تر از افزایش نقاط داخلی است. وقتی از صفحه ی گسترده استفاده می کنید، دانش آموزان ابتدا تأثیر نقاط داخلی را مشاهده می کنند.

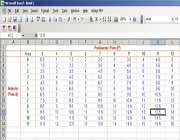
کلاس را گروه بندی کنید و از هر گروه بخواهید صفحه ی گسترده ای ایجاد کرده و مقادیر نقاط محیطی را در سطر اول و مقادیر نقاط داخلی را در ستون اول درج کنند. وقتی دانش آموزان می فهمند با مقدار 0، 1و 2 برای نقاط داخلی، هیچ شکلی نمی توانند بسازند، بحث گرمی بین آن ها ایجاد می شود. بعد از آن، می فهمند که مقادیر نقاط داخلی را باید از 3 شروع کرد. اما شکل های مختلفی با مقدار صفر برای نقاط داخلی می توان ساخت. بنابراین مقادیر نقاط داخلی از صفر شروع می شود. دانش آموزان می توانند با استفاده از برنامه ی اکسل، Quattro یا دیگر برنامه های کاربردی برای ایجاد صفحه ی گسترده بر روی رایانه، صفحه ی گسترده ای بسازند یا این که از برگه ی فعالیت صفحه ی گسترده ی پیک استفاده کنند. (با استفاده از برنامه ی ایجاد صفحه ی گسترده در رایانه، دانش آموزان پس از تعیین الگو، می توانند باقی ستون ها را به طور خودکار پر کنند.)

ممکن است گروه ها بخواهند خانه های جدول را به طور نامنظم پر کنند یا آن که به صورت منظم و به ترتیب، ابتدا سطرها و سپس ستون ها را پر کنند. البته با استفاده از روش منظم، زودتر می توان به فرضیه ی آهنگ ثابت تغییر رسید. در شکل زیر نتایج به صورت منظم و مرتب نشان داده شده است.

پس از این که دانش آموزان حدس زدند که افزایش مقادیر خانه های هر سطر به اندازه ی 2/1 واحد و مقادیر خانه های هر ستون به اندازه ی 1 واحد است، از آن ها بخواهید تا عددی را وارد جدول کنند و ببینند آیا مساحت شکلی با این اندازه ها، برابر با مقدار پیش بینی شده است یا نه. برای مثال، ممکن است یکی از دانش آموزان با توجه به الگو، حدس بزند که مساحت شکلی با 11 نقطه ی محیطی و 9 نقطه ی داخلی 2/1 13 واحد سطح است. اعضای گروه باید چنین شکلی را یافته و درستی یا نادرستی حدس دوست خود را ثابت کنند.

پس از آن که دانش آموزان با موفقیت الگو را تمرین کردند، از همه بخواهید تا در مورد آهنگ تغییر بحث کنند. سپس از گروه ها بخواهید تا با علایم جبری، برای الگوی خود، فرمولی به دست بیاورند. اگر دانش آموزان، درس های قبلی این مجموعه یعنی قضیه ی پیک به عنوان یک دستگاه معادلات و کشف الگوی قضیه ی پیک را مطالعه نکرده باشند، یافتن این فرمول برایشان دشوار خواهد بود. اما اگر این دروس را مطالعه کرده باشند، به سرعت می توانند این فرمول را به دست آورند. توجه به ضریب P می تواند بحث داغی بین دانش آموزان ایجاد کند.

با توجه به این که این ضریب، آهنگ تغییر را نشان می دهد می توان آن را به صورت r/s نشان داد که r تغییر در مساحت و s تغییر در تعداد نقاط محیطی است.

بنابراین، هر وقت تعداد نقاط محیطی به اندازه ی 1 واحد زیاد می شود، ضریب P نشان دهنده ی 2/1 واحد مربع تغییر در مساحت است. یعنی:

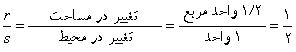
به همین ترتیب هر بار که تعداد نقاط داخلی به اندازه ی 1 واحد زیاد می شود، مساحت به اندازه ی 1 واحد مربع افزایش می یابد. پس ضریب P یک است. با این حساب فرمول به صورت زیر است: A = 1/2 P + 1 I . دانش آموزان با توجه به الگوها می فهمند که مساحت هر شکل 1 واحد کم تر از مقداری است که با فرمول محاسبه می شود. پس شکل صحیح فرمول به شکل زیر است:

A = 1/2 P + I - 1

در کلاس جبر یا حسابان، ساخت فرمول و بحث درباره ی شیب، نقطه ی توقف خوبی است. در کلاس حسابان که فضا برای تشریح مفهوم مشتق جزیی آماده است، پرسش های زیر را مطرح کنید: "مفهوم این که یک متغیر را ثابت نگه می داریم و متغیر دیگر را تغییر می دهیم، چیست؟"

محاسبه ی مشتق جزیی، بخشی از معرفی و توضیح موضوع است. معادله ی A = 1/2 P + I – 1 داده شده است. اگر I ثابت نگه داشته شود، مشتق جزئی A نسبت به P، برابر با 2/1 می شود. این نتیجه، همان پدیده ای است که دانش آموزان در صفحه ی گسترده به آن می رسند. به همین روش اگر P ثابت نگه داشته شود، مشتق جزیی A نسبت به I، برابر با 1 می شود. البته چون قضیه ی پیک پیوسته نیست، نمی توان از آن مشتق جزئی گرفت. اما مثال و بحث در مورد ثابت نگه داشتن یک متغیر در حالی که متغیر دیگر می تواند تغییر کند، م?ثر است. این موضوع را می توان برای ایجاد بحث داغی درباره ی پیوستگی به کار برد.

 

پرسش هایی برای دانش آموز

چه مقادیری برای P قابل قبول است؟ چه مقادیری برای I قابل قبول است؟

[هیچ شکلی را نمی توان با کم تر از سه نقطه ی محیطی درست کرد. بنابراین مقادیر 0، 1 و 2 برای P قابل قبول نیست. از سوی دیگر، با هر تعداد نقاط داخلی، می توان شکلی ساخت. بنابراین همه ی مقادیر صحیح برای I قابل قبول است.]

بهترین روش برای پر کردن صفحه ی گسترده چیست؟

[با توجه به این که تعداد الگوها در این جا محدود است، تکمیل سطرها و ستون های این جدول آسان است. دانش آموزان باید توجه کنند که مقادیر به اندازه ی 2/1 از یک ستون به ستون بعدی و به اندازه ی 1 از هر سطر به سطر بعدی افزایش می یابد. با این اطلاعات تکمیل صفحه ی گسترده آسان تر می شود.]

آهنگ تغییر در معادله ی ریاضی چگونه است؟

[ضریب 2/1 در جلوی P، نشان می دهد که با افزایش تعداد نقاط داخلی به اندازه ی 1 واحد، مساحت به اندازه 2/1 در تعداد نقاط داخلی افزایش می یابد. به همین ترتیب، ضریب 1 در جلوی I نشان می دهد که با افزایش تعداد نقاط محیطی به اندازه ی 1 واحد، مساحت به اندازه ی 1 واحد مربع افزایش می یابد.]

 

ارزشیابی

1-از دانش آموزان بخواهید تا نامه ای به دوست غایب خود بنویسند و ضمن راهنمایی برای انجام این فعالیت، مفاهیم کلیدی و روش های جلوگیری از اشتباه را برای وی توضیح دهند. از آن ها بخواهید تا مطالب را با ادبیاتی بنویسند که هم کلاسی شان درس را بفهمد و در صورت لزوم می توانند از مثال استفاده کنند.

2-پرسش هایی مطرح کنید که دانش آموزان مجبور شوند برای حل آن، به جای فرمول نهایی از آهنگ تغییر استفاده کنند. برای مثال "فرض کنید مساحت شکلی 2/1  4 است. اگر شکل دیگری با همان تعداد نقاط محیطی و با تعداد نقاط داخلی که 1 واحد از تعداد نقاط محیطی آن بیشتر است، بسازیم، مساحت آن چه قدر می شود؟" دانش آموزان را تشویق کنید تا بدون مراجعه به صفحه ی گسترده به این پرسش پاسخ دهند. پس از آن بپرسید: "مساحت شکلی با 10 نقطه ی داخلی بیشتر چقدر است؟ " سپس امتحانی کوتاه با پرسشی درباره ی کاربرد آهنگ تغییر برای نقاط محیطی بگیرید و از آن ها بخواهید تا راه حل مسئله را کامل بنویسند.

توسعه

1-ممکن است دانش آموزان بخواهند بعضی از ستون یا سطرهای جدول را رنگی کنند تا بعضی از الگوها را متمایز کنند. از این کار می توان برای ترسیم نمودار معادله با دو متغیر مستقل استفاده کرد. از دانش آموزان بخواهید تا از مکعب ها برای ایجاد ارتفاع در خانه های جدول صفحه ی گسترده استفاده کنند. این کار، درک مفهوم سرعت تغییر را با تغییر سطرها و ستون ها تقویت می کند.

2-از دانش آموزان بپرسید: "چه کسی می تواند این فعالیت را طوری کامل کند که آهنگ تغییر در خطی مانند y = 3x – 5

 یا y = -3/4 x + 1 را نشان دهد؟" این کار کمک می کند تا درک دانش آموزان از مفهوم آهنگ تغییر تقویت شده و دانش آموزان میان این مفاهیم و مفاهیم پیشین ارتباط برقرار کنند.

 

بررسی اجرای طرح درس در کلاس

آیا فناوری آموزشی صفحه ی گسترده نیازهای آموزشی را به صورت کامل برطرف می کند؟ آیا دوباره از این فناوری استفاده می کنید یا این فعالیت را بر روی کاغذ انجام می دهید؟

آیا دانش آموزان جدول را به صورت نامنظم پر کردند؟ آیا این کار مفید است یا باید آن ها را به سمت رهیافت منظم تری هدایت کرد؟

چگونه انتقال الگوی صفحه ی گسترده به معادله ی ریاضی، کار را ساده تر می کند؟

دانش آموزان در بحث آهنگ تغییر با چه مشکلاتی مواجه شدند؟ چگونه می توان به آن ها کمک کرد تا بیشتر درگیر بحث شوند؟